Programacion Lineal
La programación lineal es el campo de la programación matemática dedicado a maximizar o minimizar (optimizar) una función lineal,
denominada función objetivo, de tal forma que las variables de dicha
función estén sujetas a una serie de restricciones expresadas mediante
un sistema de ecuaciones o inecuaciones también lineales. El método tradicionalmente usado para resolver problemas de programación lineal es el Método Simplex.
El problema de la resolución de un sistema lineal de inecuaciones se remonta, al menos, a Joseph Fourier, después de quien nace el método de eliminación de Fourier-Motzkin. La programación lineal se plantea como un modelo matemático desarrollado durante la Segunda Guerra Mundial para planificar los gastos y los retornos, a fin de reducir los costos al ejército y aumentar las pérdidas del enemigo. Se mantuvo en secreto hasta 1947. En la posguerra, muchas industrias lo usaron en su planificación diaria.
El ejemplo original de Dantzig de la búsqueda de la mejor asignación de 70 personas a 70 puestos de trabajo es un ejemplo de la utilidad de la programación lineal. La potencia de computación necesaria para examinar todas las permutaciones a fin de seleccionar la mejor asignación es inmensa (factorial de 70, 70!) ; el número de posibles configuraciones excede al número de partículas en el universo. Sin embargo, toma sólo un momento encontrar la solución óptima mediante el planteamiento del problema como una programación lineal y la aplicación del algoritmo simplex. La teoría de la programación lineal reduce drásticamente el número de posibles soluciones factibles que deben ser revisadas.
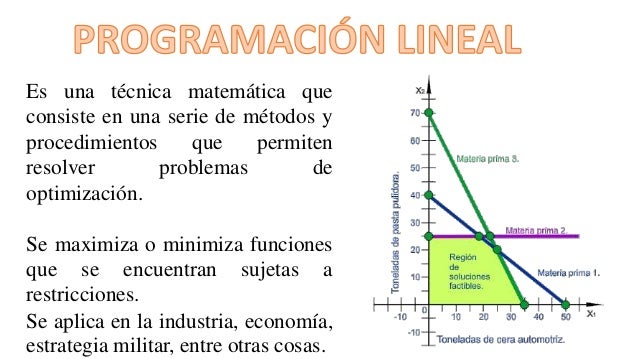
El problema de la resolución de un sistema lineal de inecuaciones se remonta, al menos, a Joseph Fourier, después de quien nace el método de eliminación de Fourier-Motzkin. La programación lineal se plantea como un modelo matemático desarrollado durante la Segunda Guerra Mundial para planificar los gastos y los retornos, a fin de reducir los costos al ejército y aumentar las pérdidas del enemigo. Se mantuvo en secreto hasta 1947. En la posguerra, muchas industrias lo usaron en su planificación diaria.
El ejemplo original de Dantzig de la búsqueda de la mejor asignación de 70 personas a 70 puestos de trabajo es un ejemplo de la utilidad de la programación lineal. La potencia de computación necesaria para examinar todas las permutaciones a fin de seleccionar la mejor asignación es inmensa (factorial de 70, 70!) ; el número de posibles configuraciones excede al número de partículas en el universo. Sin embargo, toma sólo un momento encontrar la solución óptima mediante el planteamiento del problema como una programación lineal y la aplicación del algoritmo simplex. La teoría de la programación lineal reduce drásticamente el número de posibles soluciones factibles que deben ser revisadas.

Comentarios
Publicar un comentario